BUSQUEDAS
EJEMPLOS DE
APLICACIÓN DE TÉCNICAS DE BÚSQUEDA.
Descripcion del problema:
Rompecabezas
Descripción del problema:
Todos hemos jugado alguna vez a armar un rompecabezas. Quizá recuerdes aquellos rompecabezas en los que te daban un tablero con pequeños cuadros y un espacio vacio que te permitía mover los cuadros hasta armar una figura. Si no los recuerdas, la figura de abajo seguramente refrescará tu memoria.


En la figura se muestra el mismo rompecabezas 2 veces, la primera imagen es el rompecabezas armado y la segunda el rompecabezas desarmado.
En este tipo de rompecabezas, puedes mover cualquiera de los cuadros contiguos al cuadro vacio (cuadrito blanco de la figura).
Para este problema se utilizará un rompecabezas de 9 cuadritos en una figura de 3 x 3 cuadros y un cuadro vacio. Deberas escribir un programa que dada la configuración inicial del rompecabezas determine cual es el número mínimo de pasos que se tienen que realizar para armar el rompecabezas. Se considera un paso el mover una pieza cualquiera hacia el espacio vacio.
Descripcion de la entrada:
Tu programa deberá leer del teclado la configuracion inicial del rompecabezas. La configuración inicial estará dada por una secuencia de 10 números entre el 0 y el 9, donde el 0 representa al cuadro vacio y los números del 1 al 9 representan a las piezas. Por ejemplo, la secuencia de números {1 2 0 4 6 3 7 5 8 9} representa la configuración:
| 1 |
2 |
0 |
| 4 | 6 | 3 |
| 7 | 5 | 8 |
| 9 |
Tu programa deberá buscar la forma de llegar a
| 1 |
2 |
3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 0 |
Los dos cuadros a la izquierda de la última fila no pueden utilizarse por ninguna pieza.
La secuencia de números se te dara en una sola línea con cada número separado del anterior por un espacio.
Descripcion de la salida:
Tu programa deberá escribir en la pantalla un único número que indica la cantidad mínima de movimientos que se requieren para armar el rompecabezas.
Ejemplo:
| Entrada | Salida |
| 1 2 0 4 6 3 7 5 8 9 | 5 |
Condiciones de ejecucion.
Tu programa debera ejecutarse en un tiempo maximo de 1 segundo.
Estructura de la solución: ¿Qué nos están
pidiendo? El número mínimo de
movimientos para llegar de una permutación inicial de los números {0..9} a la
permutación {1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, utilizando únicamente los
movimientos permitidos por el problema.
Es decir, acomodar los números sobre el tablero y mover el 0 ya sea
hacia arriba, abajo, izquierda o derecha según sea posible.
Modelo del espacio de búsqueda como árbol: La raíz de nuestro árbol es el tablero
inicial, en cada nodo, dependiendo de la posición del cuadro vacío {0}, se
podrá pasar a 1, 2, 3 ó 4 nuevos estados.
Por lo que nuestro árbol de búsqueda quedaría de la siguiente
forma: en la raíz, el tablero inicial,
como hijos de la raíz cada uno de los estados a los que se puede pasar por
medio de un movimiento permitido, etc.
El árbol se muestra en la figura de abajo.
| 1 | 2 | 0 |
| 4 | 6 | 3 |
| 7 |
5 |
8 |
| 9 |
| 1 | 0 | 2 | 1 | 2 | 3 | ||||||||||
| 4 | 6 | 3 | 4 | 6 | 0 | ||||||||||
| 7 | 5 | 8 | 7 | 5 | 8 | ||||||||||
| 9 | 9 |
| 0 | 1 | 2 | 1 | 2 | 0 | 1 | 6 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 0 | ||||||||||
| 4 | 6 | 3 | 4 | 6 | 3 | 4 | 0 | 3 | 4 | 0 | 6 | 4 | 6 | 8 | 4 | 6 | 3 | ||||||||||
| 7 | 5 | 8 | 7 | 5 | 8 | 7 | 5 | 8 | 7 | 5 | 8 | 7 | 5 | 0 | 7 | 5 | 8 | ||||||||||
| 8 | 9 | 9 | 9 | 9 | 9 |
Técnica de búsqueda a utilizar: Para este
problema no solo queremos llegar a la solución, sino que necesitamos saber cual
es el número mínimo de movimientos
para llegar a la solución, dado que cada nivel en el árbol de búsqueda
representa un movimiento, la solución más cercana a la raíz es la solución que
buscamos. Y cuando necesitamos la
solución más cercana a la raíz utilizamos búsqueda en amplitud.
Detalles de implementación: Una búsqueda en amplitud se implementa
utilizando una cola en la que se introducen uno a uno todos los nodos a los que
se puede llegar desde el nodo que se esta procesando. Para este caso en particular, cada estado nos puede llevar a un
máximo de 4 nuevos estados, dado que no conocemos si existe un limite teórico
para el número de movimientos que nos llevan a la solución no sabemos cual es
la profundidad a la que tendremos que descender para encontrar una solución.
Una forma de implementar nuestra solución sería
representar cada estado como un arreglo de 10 bytes, tomando el peor caso de
crecimiento, es decir 4 nuevos estados por cada estado, para una profundidad de
10 movimientos requeriríamos de un total de memoria de 410 arreglos
de 10 bytes, es decir aproximadamente 10MB, para 12 movimientos requeriríamos
de 160MB y para 13 de 640MB. Aunque
quizá muchos tableros se puedan resolver en menos de 10 movimientos (el del
ejemplo es uno de ellos), seguramente hay algunos que necesitan mas, y en esos
casos nuestra solución no resultaría posible de implementar por limitaciones de
memoria (recuerden el caso de la aguja en el pajar, necesitábamos un cuarto lo
suficientemente grande). Necesitamos
por lo tanto hacer algo para reducir la cantidad de memoria que necesitamos.
Una de las formas más comunes de reducir el espacio
de búsqueda en una búsqueda por amplitud es el almacenar los estados que ya han
sido revisados para no volverlos a revisar.
Siempre que se
aplica una poda, debe revisarse antes que esta poda no elimine alguna posible
solución. En el caso de esta poda,
podemos estar seguros de que al aplicarla no eliminamos ninguna solución por la
siguiente razón, si llegamos a un estado que ya habíamos revisado anteriormente
quiere decir que había una manera más corta de llegar a dicho estado, por lo tanto
hay una manera mas corta de llegar a todos los estados que se deriven de
él. Como estamos buscando la manera mas
corta de llegar a la solución, entonces podemos eliminar dicho estado y todo su
subárbol sin miedo a eliminar una posible solución mejor.
Si revisamos con más cuidado el árbol de la figura,
veremos que de cualquier estado siempre se deriva uno que es idéntico a su
padre, el cual surge de “regresar” el último movimiento. Este estado siempre puede ser eliminado, ya
que nos lleva a un estado previamente visitado. Tomando esto en cuenta, entonces nuestro espacio de búsqueda ira
creciendo máximo 3 nuevos estados por cada estado en vez de 4. Si de nuevo utilizamos la representación de
10 bytes para cada posible estado tenemos que para 13 movimientos necesitamos
apenas 16MB, sin embargo, aunque esta mejora nos aumenta algunos movimientos,
difícilmente podremos pasar de 15 movimientos lo cual pudiera no ser
suficiente. Necesitamos pues alguna
otra poda.
De nuevo hay que analizar el espacio de búsqueda para
encontrar formas de optimizar la búsqueda (este procedimiento es algo que tendrás que
realizar constantemente con todos los problemas, hasta que estés seguro que
tienes la mejor solución o que tu solución es suficientemente buena para las
restricciones de tiempo y memoria del problema). Con nuestra poda anterior eliminamos algunos de los nodos
repetimos, sin embargo no se eliminaron todos los nodos repetidos, únicamente
aquellos que “regresaban” el último movimiento. Para poder eliminar todos los movimientos repetidos requerimos
de tener almacenados en algún lugar todos los nodos que ya hemos revisado, de
modo que para cada nodo nuevo podamos verificar si se encuentra entre los
anteriormente revisados y de ser así eliminarlo. Como no sabemos cuales nodos vamos a revisar, necesitamos
espacio suficiente para almacenar entre los revisados todos los estados
posibles, ya que en el peor de los casos la solución podría ser el último
nodo que revisáramos, una vez que todos los estados anteriores ya han sido
revisados.
La siguiente pregunta que debemos hacernos por tanto
es ¿Cuántos estados posibles hay en nuestro problema? Dado que cada estado se representa por una permutación de 10
números, la cantidad de estados posibles es de 10! ≈ 3.6 millones, si a cada uno de estos estados lo
representamos como un arreglo de 10 bytes, entonces tenemos que necesitamos un
total de 36MB para almacenar los estados visitados, además necesitamos memoria
para la cola, como en el peor de los casos vamos a introducir cada estado en la
cola solamente una vez, entonces la cola jamás contendrá mas de 10! Elementos,
lo que nos indica que con otros 36MB tenemos suficiente para la cola, esto nos
da un total de 72MB máximo, sin importar la cantidad de movimientos necesarios. Si
bien, esto es una cantidad de memoria grande, al menos es una cantidad de
memoria realista.
Podríamos pensar que ya tenemos nuestra solución
ideal para el problema, pero todavía queda un pequeño detalle por
resolver. Todavía necesitamos saber
como vamos a buscar si un nuevo estado se encuentra entre los estados
previamente revisados. Como nuestra
representación de un estado es un arreglo de 10 bytes, tenemos varias opciones
que se enumeran a continuación:
·
Cada
que tengamos un nuevo estado simplemente lo agregamos a una lista de estados
visitados: Si utilizamos este método,
cada que queramos revisar si algún estado se encuentra en la lista tendremos
que revisar toda la lista, lo cual nos llevará un tiempo proporcional al número
de elementos de la lista, y esto tendremos que hacerlo para cada nuevo
estado. Como el número de elementos de
la lista puede ser hasta de 10! y el
número de estados que podemos revisar es también de hasta 10! esto nos da que
en el peor caso teórico tendríamos que revisar (10!)(10!) , mas de
10,000,000,000,000 veces. Obviamente
esta solución no es viable por tiempo.
·
Cada
que tengamos un nuevo estado agregarlo a una arreglo ordenado: Buscar en una
arreglo ordenado se puede llevar a cabo con una búsqueda binaria en tiempo
logarítmico esto nos reduciría el numero de búsqueda a (10!) log (10!)
aproximadamente 75,000,000, esto ya es realizable por una computadora moderna
en fracciones de segundo. Sin embargo
introducir un elemento en una arreglo ordenado nos lleva un tiempo proporcional
al tamaño del arreglo, por lo que si bien la búsqueda es rápida, la inserción
de cada nuevo elemento vuelve a ser cuadrada del orden de millones de millones.
·
Utilizar
un árbol binario de búsqueda para almacenar los estados visitados: Esta solución ya es mucho más viable, ya que
un árbol de búsqueda requiere de un tiempo logarítmico tanto para buscar un
elemento como para insertar uno nuevo.
Sin embargo, aunque sería suficiente para el caso promedio pueden
existir casos en los que el árbol de búsqueda quede degenerado y el tiempo de
acceso e inserción no sean logarítmicos.
·
Utilizar
un árbol binario de búsqueda balanceado para almacenar los estados visitados: Esta solución nos
asegura un tiempo logarítmico de acceso e inserción sin importar cual sea el
caso de prueba, sería por lo tanto la mejor de todas las soluciones y la única
que tendría esperanzas de correr tanto en espacio como en tiempo.
El análisis anterior no es muy alentador, la única
solución viable es utilizar una estructura de datos avanzada lo cual dificulta
bastante la implementación y la hace muy propensa a errores. ¡Debe existir algo mejor!
Aquí llegamos al punto más importante de la
implementación de una búsqueda, ya definimos nuestro espacio de búsqueda, ya
sabemos donde buscar y que es lo que estamos buscando, ahora tenemos que
introducir todo nuestro modelo a una computadora y nos topamos con la siguiente
cuestión ¿Cuál es la
mejor manera de representar nuestro modelo en una computadora?
Volvamos una vez más al análisis del problema, en
total tenemos 10! estados, esto es menos de 4 millones de estados. Un entero sin signo de 32 bits puede
representar enteros desde el 0 hasta mas de 4,000,000,000. Mucho mas que lo que necesitamos. Dado que cada estado es único, ¿No existirá
la manera de asignarle a cada estado un número entero? Si fuera posible, entonces bastaría con
tener un arreglo de 3.6 millones de boléanos para representar los estados
visitados, si el valor de esa permutación tiene verdadero entonces ya ha sido
visitado, si tiene falso no ha sido visitado.
La memoria total que necesitaríamos para el arreglo de visitados sería
de 3.6MB y para la cola necesitaríamos máximo 3.6 millones de enteros de 32
bits, lo que nos da un total de 18MB para la cola y el arreglo. ¡Esto suena mucho mejor! Además, el tiempo para verificar si un
estado ha sido revisado o para marcar un estado como visitado, una vez que se
tiene su representación numérica, sería constante lo cual es mucho mejor que el
tiempo logN que obteníamos con la solución del árbol
balanceado. Por lo tanto si podemos
representar cada estado como un número entero único, tendremos una solución que
es mucho mejor en memoria y en velocidad.
Tenemos ahora un nuevo problema. ¿Cómo asignar un número entero único a cada
una de las permutaciones?
Estructura de la
solución: ¿Qué nos están pidiendo?
Una función f(X) → Z+ , es decir, una función que
reciba como parámetro de entrada una permutación y nos entregue como resultado
un número entero.
Modelo del espacio
de búsqueda como árbol: En la
primera sección se propuso un árbol para crear todas las permutaciones de N números, donde cada camino
desde la raíz hasta una hoja representaba una permutación. La figura se muestra abajo.
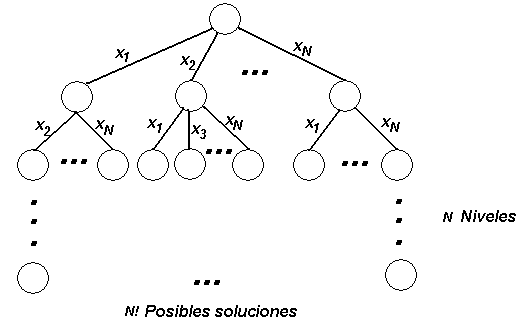
Búsqueda a
utilizar: Una posible idea para enumerar
las permutaciones es la siguiente. Si
numeramos las hojas del árbol de izquierda a derecha, con los números del 1 al N! lo único que tenemos que hacer para obtener nuestra función es
tomar nuestra permutación de entrada e ir recorriendo las ramas del árbol de
acuerdo a los elementos, cuando lleguemos a una hoja podremos saber que número
de permutación es.
Detalles de
implementación: Antes de leer esta
sección, te recomiendo tratar de hacer tu propia implementación utilizando la
idea anterior. Cuando la tengas sigue
leyendo.
Contrario a lo
que parece a primera vista, la implementación de la idea es muy sencilla. La idea principal es la siguiente: El árbol para formar permutaciones que se
presento anteriormente tiene N! hojas para N niveles, como la
estructura se mantiene, esto quiere decir que un árbol de (N-1) niveles tendrá (N-1)! hojas. Esto es, cada uno de los hijos de la raíz es
a su vez la raíz de un subárbol que tiene (N-1)! hojas. ¿De qué nos sirve esto? Bueno, es sencillo, si el primer elemento de
la permutación de entrada es el hijo i de la raíz, entonces sabemos que en los hijos
anteriores a i tenemos en total
(i-1)(N-1)! hojas. Teniendo este dato, podemos recursivamente
hacer lo mismo con el nuevo árbol.
La implementación
en pascal es la siguiente:
Type
TPermutacion
= array[1..10] of byte; // EN PASCAL ES NECESARIO DECLARAR
//
UN TIPO DE DATOS PARA PODER PASAR
//
UN ARREGLO COMO PARÁMETRO
const
Fact : array[1..10] of integer =
(9!,8!,7!,6!,5!,4!,3!,2!,1!,0!); // EN UNA IMPLEMENTACION REAL
// DEBEN SUSTITUIRSE ESTOS NUMEROS
POR LOS VALORES REALES, PERO POR
//
LEGIBILIDAD DEL EJEMPLO SE UTILIZARON ASI.
RECUERDA QUE POR
//
CONVENCIÓN 0! = 1.
Function NumeroDePermutacion(Permutacion
: TPermutacion) : integer;
Var
i, j, k : integer;
ElementosNoUtilizados : array
[1..10] of integer; // NECESITAMOS ESTE ARREGLO PARA
//
SABER QUE ELEMENTOS HEMOS UTILIZADO
NElemNoUtilizados : integer;
Res : integer; // EN ESTA VARIABLE
LLEVAMOS EL RESULTADO.
Begin
Res:=0;
// PRIMERO HAY QUE CARGAR TODOS LOS
ELEMENTOS DE LA PERMUTACION COMO NO UTILIZADOS
for i:=1 to 10 do
ElementosNoUtilizados[i]:=X[i]; //
CARGA LOS ELEMENTOS ORIGINALES
NelemNoUtilizados:=10;
// DE INICIO HAY 10 ELEMENTOS QUE NO HAN SIDO UTILIZADOS.
//
AHORA VAMOS A BUSCAR LA PERMUTACIÓN
for
i:=1 to 10 do begin // PARA TODOS LOS
ELEMENTOS DE LA PERMUTACION
for
j:=1 to NelemNoUtilizados do // CALCULA QUE NUMERO DE HIJO ES
if
ElementosNoUtilizados[j] = Permutacion[i] then begin
Res:=Res
+ (j-1)*Fact(i); // AGREGA TODAS LAS HOJAS DE LOS
//
SUBARBOLES ANTERIORES
//
POR ULTIMO, HAY QUE ELIMINAR ESE ELEMENTO DE LOS NO UTILIZADOS
for k:=j to Pred(NelemNoUtilizados) do
ElementosNoUtilizados[k]:=ElementosNoUtilizados[k+1]; Dec(NelemNoUtilizados);
break;
end;
end;
NumeroDePermutacion:=Res; // POR
ULTIMO DEVUELVE EL RESULTADO.
End;
La rutina
anterior obtiene el número de permutación en un tiempo proporcional a N2, existen formas
de mejorar esto a N
log N utilizando estructuras de datos muy avanzadas para el manejo de los
elementos no utilizados, sin embargo para permutaciones de N=10 no hay mejora perceptible,
sin embargo para permutaciones de muchos mas elementos se tendría que utilizar
dicha técnica. Un tip importante es que si la
solución que tienes es suficiente para resolver lo que te piden, no es
necesario buscar soluciones más óptimas, y en general más complicadas.
Teniendo la función para enumerar permutaciones, la
implementación de la búsqueda en amplitud resulta sencilla, y se presenta a
continuación (queda para el alumno las tareas de implementar las funciones
faltantes para manejo de la cola)
var
EstadosVisitados
: array [0..10!] of boolean; // AQUI SE ALMACENAN INICIALMENTE LOS ESTADOS
VISITADOS.
PermutacionEntrada,
Ptemporal, SigEstado : Tpermutacion;
Movimientos
: integer;
i :
integer;
begin
PermutacionEntrada:=LeePermutacionDeEntrada(); // LEE LA PERMUTACION DE ENTRADA DEL
PROBLEMA
InsertaEnCola(PermutacionEntrada,0);
// INSERTA EN LA COLA INDICANDO CUANTOS MOVIMIENTOS SE REQUIEREN
//
PARA LLEGAR A ESE ESTADO
while Not(ColaVacia) do begin
Ptemporal:=SacaDeCola(Movimientos);
// LA FUNCION SacaDeCola DEBE DEVOLVER LA SIGUIENTE
PERMUTACION
//
EN LA COLA Y EL NUMERO DE MOVIMIENTOS QUE SE NECESITAN PARA LLEGAR
//
A DICHO ESTADO.
if Ptemporal = PermutacionSolucion then begin
// SI ES LA PERMUTACION SOLUCION YA
TERMINAMOS, EL RESULTADO FINAL ES EL NUMERO
//
DE MOVIMIENTOS QUE SE NECESITARON PARA LLEGAR
EscribeResultado(Movimientos);
exit(0); // TERMINA EL PROGRAMA
end
else begin
// SI NO SE HA ENCONTRADO LA
SOLUCION HAY QUE HACER VARIOS PASOS
//
PRIMERO MARCAR COMO VISITADO EL ESTADO
EstadosVisitados[NumeroDePermutacion(Ptemporal)]:=true;
//
DESPUES METER A LA COLA TODOS SUS HIJOS, SIEMPRE Y CUANDO ESTOS NO HAYAN SIDO
//
VISITADOS ANTERIORMENTE.
for i:=1 to 4 do begin
SigEstado:=SiguienteEstado(Ptemporal,i);
// LA FUNCION SIGUIENTE ESTADO GENERA
//
LOS NUEVOS ESTADOS MOVIENDO EL ESPACIO VACIO HACIA
//
ARRIBA, ABAJO, DERECHA O IZQUIERDA. SI
EL ESTADO
//
NO ES POSIBLE DEVUELVE COMO RESULTADO EL MISMO ESTADO
if
Not(EstadosVisitados[NumeroDePermutacion(SigEstado)]) then
InsertaEnCola(SigEstado,Movimientos
+ 1);
end;
end;
end;
end.
Como se puede ver, la implementación de la búsqueda
es sencilla, de apenas unas 10 – 15 líneas si se eliminan los comentarios. Hay un punto importante que observar en la
implementación anterior, en la cola se están insertando las permutaciones
completas, es decir, arreglos de 10 bytes, esto obliga a apartar del orden de
unos 16MB mínimo para la cola, si queremos insertar en la cola, no la
permutación sino su número, necesitamos entonces una función que a partir del
número de permutación. Esta función
es sencilla y muy parecida a la que calcula el número de la permutación. Queda para tarea del alumno realizar dicha
implementación.